Mahendra Prasad: Rational group decision-making

Effective altruism aims to help individuals improve their decision-making, but the topic of decision-making in groups often falls by the wayside. In this talk from EA Global: London 2019, Mahendra Prasad, a PhD candidate at the University of California, Berkeley, focuses on two aspects of group decision-making: ways to aggregate information from individuals within a group and conditions under which groups tend to make better decisions.

Below is a transcription of Mahendra’s talk, which we’ve lightly edited for clarity. You can also watch it on YouTube and discuss it on the EA Forum.

The Talk

Why does this talk matter?

Improving group decision-making procedures at the highest levels affects all downstream decision-making. So if we’re thinking about [working toward one kind of] institutional reform, it's the most effective thing we can do.

I have two sections [I’ll cover in this talk]:

1. Improving the aggregation of individual opinions to make group decisions
2. Improving the background conditions under which such decisions are made

I discuss a lot of this in much more detail in my paper “A Re-interpretation of the Normative Foundations of Majority Rule.” [In this talk,] I'm just going to go over the very basic details.

Improving the aggregation of individual opinions to make group decisions

I think there are certain social-choice results that pretty much everybody should be familiar with — especially effective altruists.

I think that one of them is probably the most important theorem in all of social science: the Gibbard-Satterthwaite theorem. (I can't go into detail with any of these theories because of time constraints, but I really encourage people to look them up.)

Others are Gibbard's non-deterministic theorem, the Muller-Satterthwaite theorem, May's theorem, and Arrow's theorem.

One result that I am going to go over in detail is something called Condorcet's paradox. There are a few things that we have to follow with respect to Condorcet's paradox. One is the idea of intransitivity. In very straightforward terms, if the group decides to do A over B, and they also choose B over C, then this should imply that they prefer A over C. It's intransitive if it doesn't follow those basic rules.

Another important concept to be familiar with is something called “independence of irrelevant alternatives” (IIA). For example, let's say you have a group of housemates trying to choose which tub of ice cream to purchase for a house party they're having. The vendor says, “We have two tubs: one that's vanilla and one that's chocolate.” The group decides to go with chocolate.

Now, let's say the vendor says, “Wait a second — I just realized I also have strawberry.” We would think that the rational thing for [the housemates] to do would be to choose between chocolate and strawberry. They'd violate [the concept of] independent of irrelevant alternatives if they said, “Now our top choice is vanilla.”

That's basically the idea — that if we're comparing two alternatives, the introduction or removal of a third separate alternative should not affect our decision on [the original] two alternatives.

This is a very important aspect of group decision-making if we want to behave in accordance with the von Neumann-Morgenstern utility function.

I’ll quickly go over two other concepts. One is called a “Condorcet winner” and the other is a “Condorcet method.” A Condorcet winner is an alternative that beats all other alternatives one-on-one, via majority preference. A Condorcet method is one that always guarantees the election of a Condorcet winner when one exists.

So basically, a Condorcet paradox is when a Condorcet method exists that satisfies both transitivity and independence of irrelevant alternatives.

This is the classic example to demonstrate this concept:

Imagine that we have three voters and three alternatives. The first voter prefers A over B over C. The second voter prefers B over C over A, and the third voter prefers C over A over B. What you'll notice is that the majority prefers A over B — namely, the first voter and the third voter. And a majority prefers B over C — namely, the first voter and the second voter. If majority preference were transitive, then this would imply that the majority prefers A over C. But you can see that the second and third voters prefer C over A.

This is kind of like saying that 30 is greater than 20, and 20 is greater than 10, so 20 is greater than 30. It makes the idea of a top social preference meaningless. So it's a very important result.

If you're interested in learning more about social choice, here is some literature you might want to take a look at:

In any case, the main goal of my discussion with respect to improving aggregation is to argue that the normative arguments from a majority rule on two alternatives cannot be well-generalized with majority preference. But they can be well-generalized with another conception: consent of the majority.

It's pretty clear why it can't be done with majority preference. This is well understood in the literature. It's because it violates transitivity or IIA. It’s Condorcet's paradox. And majority preference has been the standard interpretation of majority rule since roughly the 1950s.

But there’s another way of interpreting majority rule: “consent of the majority.”

Think of each alternative as a potential contract. If a voter is willing to consent to that particular contract, then they approve of it, but if they're not willing to consent to it, then they don't approve of it. With approval voting, whichever alternative is consented to or approved of by the greatest number of voters wins the election. In other words, you choose the candidate to whom the greatest number of voters consent.

We can distinguish between majority preference and consent to the majority with the following paradox. Let's say we have three friends, and two of the friends prefer pepperoni pizza over cheese pizza, and one of the friends prefers cheese pizza over pepperoni pizza. However, what they like and what they want to consent to varies. Two of the friends would consent to either pepperoni or to cheese, because they like both. But the third friend, for whatever reason, only consents to cheese. They could be vegetarian or something. And what we'll notice is that the majority preference is for pepperoni, but it lacks unanimous consent. On the other hand, all three would consent to cheese pizza.

This shows that majority preference can [result in] an alternative that does not have unanimous consent, even though a candidate exists who has unanimous consent. Importantly, approval voting satisfies both transitivity and IIA, so it can overcome Condorcet's paradox.

At this point, let’s look at what the history of philosophy says about majority rule. I'm going to flash various philosophers’ quotes up — people like John Locke, Nicholas de Condorcet, John Rawls, and Jean-Jacques Rousseau.

I'm going to focus on the Rousseau quote. He says, “When any law is proposed in the assembly of the people, the question is … if it is conformable or not to the general will.” Notice that he's not asking whether or not the proposal better conforms with the general will than with the status quo. That would be a preference question. He's basically asking a consent question — if it conforms, you consent, and if it doesn't conform, you don't consent. This lends itself to a majority-consent interpretation as opposed to a majority-preference interpretation, which you can see in the other quotes as well.

At this point I think it would be good to move on. What are the main normative arguments for majority rule on alternatives? They primarily [include] a procedural argument (which is May's theorem), an epistemic argument (which is Condorcet's jury theorem), a utilitarian argument (which is the Rae-Taylor theorem), a Contractarian argument, and a statistical argument (basically the median voter theorem).

These arguments were collected from pretty standard work. Three are in the Stanford Encyclopedia of Philosophy and four are in [Democracy and Its Critics] by Robert Dahl, who's probably the biggest political scientist of the late 20th century.

Now I'm going to discuss a few of these generalizations in detail (if you're very interested in details, you can always go to my paper, “A Re-interpretation of the Normative Foundations of Majority Rule”).

Here’s a generalization of May's theorem: Approval voting is the voting system with the least restricted domain, which satisfies IIA and May's theorem for conditions, decisiveness, anonymity, neutrality, and positive responsiveness. If you don't know what those are, don't worry about it.

The statistical argument is this: Approval voting maximizes a measure of central tendency. So the typical argument is something called “Black's median voter theorem for Condorcet's methods,” and it makes a lot of assumptions about voters and about the issue space. On the other hand, with approval voting, you don't need all of that. You can use a very simple set theoretic measurement. Each voter is a set, and if a voter approves of a particular alternative, then that alternative belongs to that voter set. If they don't approve of it, it doesn't belong to their set. So basically, the approval winner is the candidate who occurs at the largest intersection of sets. It's a very simple measure of central tendency that's being maximized.

The important [point that emerges from] all of these technical theorems is that for all of the main arguments [that apply to] majority rule for two alternatives, we can generalize very easily to multiple alternatives with approval voting. But in majority preference, because of Condorcet's paradox, we can't do that.

Now I'm going to move into some of the real-world implications of this. Because of the Citizens United ruling in the United States back in 2010, we basically have nomination processes that have large numbers of candidates in presidential elections. That increases the chances — because we use plurality voting — that the candidate who wins has only a small base of support. But it's a very intense one.

The best example of this is the 2016 presidential election. For a lot of people, this might be the most important slide of the day, so I'm going to go into detail about this data. I should mention that I got this idea from Mohit Shetty, who wrote a piece about the election in the Huffington Post. This [slide shows] data from surveys done by NBC News and the Wall Street Journal back in 2015 and 2016. [They conducted] monthly polls — in March 2015, June 2015, and so forth — and the number of candidates corresponds to each poll. For example, when the poll was taken in March 2015, there were 14 Republican candidates. When it was done in February 2016, there were six Republican candidates.

The population sample for these polls was drawn from Republican voters, so it's representative of the national population of Republican voters. Democratic voters and independent voters were not involved in this.

The questions they asked were:

• Mark each candidate that you’re willing to support. That's basically an approval-voting question [we can use to gauge] Trump support.
• Which candidate is your top preference? That's basically a plurality-voting question [to gauge Trump support].

[These questions] basically show how Trump would place in an approval-voting [versus a plurality-voting] election.

If we look at the plurality-voting contest, from July 2015 [onward], he's always in first place. It’s usually with a narrow minority — like 20-30% of Republican voters — but he still has the plurality of votes. But if you look at [whom voters are willing to support, i.e., through a plurality-voting lens], he never places first among Republican voters.

Keep in mind that in the very beginning of May 2016, Trump won the nomination because he had won enough delegates. So the March and April polls were basically the last ones before that. He won first place in both of them with plurality voting, but with the approval-voting structure, he would have been in last place: fourth out of four and tied for last out of three candidates.

So plurality voting and approval voting are two different generalizations of majority rule, and they lead to two very opposite outcomes. This is why voting systems really matter. I can't emphasize that enough.

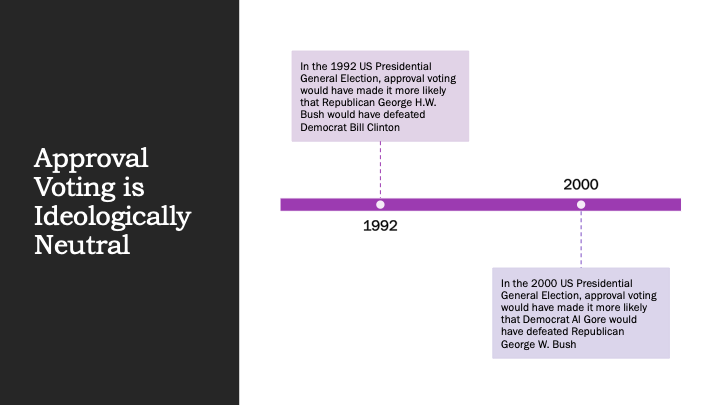
Another thing I want to emphasize is that [approval voting is] ideologically neutral. In 1992, approval voting probably would have helped the Republican candidate win. But in 2000, approval voting probably would've helped the Democratic candidate win — the point being that it's not ideologically biased in any particular direction.

I want to make a prediction that you can hold me accountable to: Given the plurality structure and the nomination process, I'm predicting that for the 2020 Democratic nomination for president, no candidate will receive a majority of regular delegates. I think that the decision will be made either by non-elected super delegates or by a contested convention. You can test me on that and see if I'm right.

So basically, with respect to improving aggregation, there are three takeaways [that I’ve presented]:

1. Unlike majority preference, consent of the majority maximizes our ability to satisfy the various normative arguments, but also generalizes to multiple alternatives.
2. Approval voting is consistent with historical interpretations of majority rule.
3. Approval voting can help us avoid vote-splitting like we experienced in the 2016 election.

Improving the background conditions under which group decisions are made

Now I'm going to talk about improving background conditions.

If people are forced to vote in a particular way, it doesn't matter which aggregation function is used. [That leads to my next point:] The background conditions under which voting occurs make a big difference. I'm going to talk about a lot of this with respect to intelligence explosion hypotheses, but it's not dependent on those. They're just historically intertwined in terms of the research.

Much of this section [of my talk] covers two of my publications: “Social Choice and the Value Alignment Problem” in the book Artificial Intelligence and Safety Security and my article in AI Magazine, “Nicholas de Condorcet and the First Intelligence Explosion Hypothesis.”

Ray Kurzweil is a director of engineering at Google and probably the most famous proponent of intelligence explosion. Among his several predictions, two are basically that (1) knowledge and technology growth are accelerating, and (2) that human lifespans can be indefinitely extended into the future. That's interesting.

What's also interesting is that Condorcet [came to that conclusion] in the 1700s. What's even more interesting is that he mathematically modeled it with his Jury theorem. So how does this theorem go? The simplest version of it [can be explained this way]:

Let’s say you have a set of N agents and they're confronted with a statement that's in one of two states: true or false. We assume that each agent has a probability (P) greater than 50% of being correct, that each agent is independent in making their judgments, and that each agent is honest about their determination. The Jury theorem says that as you increase the number of agents, the probability that the majority is correct approaches the numeral 1. It's basically an application of what's now the law of large numbers, which Condorcet didn't have access to.

A simpler way of putting this is that if voters are sufficiently honest, knowledgeable, independent-thinking, and numerous, then a majority rule is almost always correct.

So basically, what Condorcet said was we want to make society into a multi-agent system that's accelerating towards judgment. Therefore, we need institutional change. He believed that we need to improve honesty in society, and that we shouldn't [tolerate] dishonesty except when it improves honesty in the long run. Examples of institutions that promote honesty are things like contract law.

[He promoted] institutional changes [that advance] knowledge — for example, a free press and universal free schooling. And we can think of modern examples of this in terms of the work of people like Phil Tetlock on super forecasting and the work of the Center for Applied Rationality (CFAR). Both [Tetlock and representatives from CFAR] have given talks at EA Global [view Tetlock’s talk and one by Duncan Sabien of CFAR], so the effective altruism community is doing a lot of work related to this.

Condorcet wanted [more] independent thinking. One of my favorite examples [of the changes he advocated involves voting]. When masses of people voted, he didn't want them to meet in assembly. He thought they should vote by mail, because he believed that if people meet in assembly, then they form parties. And if they form parties, then they're going to stop thinking independently. That would have been more likely by mail, because back then, long-distance communication was difficult. And we can see in contemporary research that things like having a devil's advocate in meetings [makes it less likely that we] fall into groupthink.

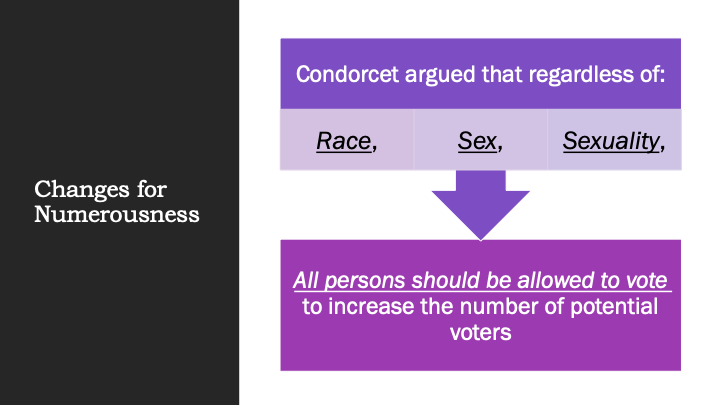
Another thing that Condorcet argued was that regardless of race, sex, or sexuality, everybody should be allowed to vote. This would increase the number of voters and let us get closer to the axiomatic approach [where the probability of a correct majority decision becomes 1].

A lot of this is discussed in _Sketch _[for a Historical Picture of the Progress of the Human Mind]. The math isn't discussed in Sketch, and that's why it has taken so long for people to figure this out. But Sketch is probably his most famous philosophical work. In it, he basically argues that societies that tend to fulfill the Jury theorem, or at least have institutions that promote the conditions of the Jury theorem, tend to be ones where knowledge and technology grow at a fast rate. So he was thinking of places like Athenian democracy and the Roman Republic.

Sites that don't have this property, like late-antiquity European societies, tend to have reversed or slowed growth in knowledge and technology. But he argues that in the long run, because of various technological changes like the printing press, human knowledge and technology are growing at an increasing rate over time.

There are several people who have generalized the Jury theorem. I've given you a set of these people and they have very excellent papers, which I encourage you to look at if you get the chance. But I think we should focus less on trying to generalize the Jury theorem, and more on [its application to] multi-agent systems. That's actually what Condorcet did.

He developed several theorems in terms of information aggregation. He even [devised] theorems where, if you have a certain set of background conditions, you probably want to use minority rule instead of majority rule.

An example showing how the multi-agent framework is helpful, I think, is a preschool. Let's say you have a class of preschoolers — three-year-olds. You also have an adult teacher. And we'll assume that the teacher is knowledgeable about crossing roads and the students aren't knowledgeable about crossing roads, or at least aren’t very knowledgeable about it, and the goal is for them to figure out when to cross the road. We'll also assume that among the three-year-olds, there's a four-year-old who bullies all of the other kids. Whatever the opinion of this bully is becomes the opinion adopted by all of the other students.

One question given these background conditions is: What is the best way to aggregate information? We can pretty clearly say that majority rule is not going to work, and we can say this because there's low information and the opinions are highly dependent on the opinions of the bully. So majority rule is going to be pretty bad in that situation.

In fact, we would probably say that you want a dictator — that dictator being the teacher who's the adult, and the people being the three-year-olds being lorded over.

A second question is: If we want the group to use a particular decision-making method, how should we change the background conditions to make the method effective?

Let’s say our goal is to make sure that each of the students can individually decide when to cross the road. We want to implement institutions that decrease the dependence of the students on the bully's opinion and increase the students' knowledge of crossing the road. This might take a few years, but [we can identify] the institutions we want in place so that the three-year-olds will start making this judgment independent of one another. Maybe after five years, when they're eight, they can figure out when to cross the road and when not to cross the road. So, the multi-agent model helps us actually formalize this whole idea.

There are two basic questions that this multi-agent modeling can be very appropriate for:

• How should we aggregate information when confronted with a particular set of background conditions?
• How should we change conditions if we want to use particular information aggregation methods?

You might say that the multi-agent framework is overkill when you're dealing with this preschool class, or when you're dealing with the classic Jury theorem conditions. But that's because they're corner cases for simple illustration. When you deal with really complex, real-world situations, you're going to have a lot of interweaving interdependencies in judgments. You're going to have a lot of varying levels of knowledge, and it's going to get very complex very quickly — basically a combinatorial explosion — and you're going to have to use approximation algorithms.

Here I lay out a very oversimplified model for what you might do. But unfortunately, the vast majority of cases are going to require approximation algorithms. Even though it's pretty obvious that you're going to need algorithmic game theory to approximate solutions, to my knowledge, there are no applications of algorithmic game theory to any of these multi-agent, system-type problems.

There [have been some applications] to other kinds of problems that require the epistemic aggregation of information, but not to problems that deal with people with dependencies and things of that nature. I think this is a big area needing a lot of research.

To give you an idea of how important this multi-system research is, [I’ll tell you a story]. There was a course taught [at UC Berkeley] in fall 2018 called “Safety and Control for Artificial General Intelligence (AGI).” And 25 of the 28 sessions for that class — 93% of them — were focused on two agents or multi-agent systems. This class is taught by Andrew Critch and Stuart Russell. I think multi-agent agents are very important for AGI control, not just for improving human decision-making.

There are several problems that these multi-agent systems could be used to address. One is the “expert independence problem.” Presumably, if we become overly reliant on experts — for example, if Democrats only do whatever an MSNBC commentator says, and [Republicans] only do whatever a Fox news commentator says — then our judgments are going to collapse. And so the question is: What are the appropriate background conditions and appropriate aggregation methods for relying on experts?

Another question involves deliberation and groupthink. There's a lot of empirical evidence showing that deliberation improves group decision-making, but we can also see cases in which people start interacting with each other and form a mob mentality. So the question becomes: Under what conditions does a mob develop? And what situations [lead to] deliberation that actually improves judgment? Multi-agent modeling [can determine] the background conditions for aggregating information to avoid this mob mentality while [also enabling] good sharing of information to make better judgments.

Our third question, which comes from John Dryzek, involves the issue of deliberation and intermittent polling. Presumably, it might be of interest to poll people during the process of deliberation, just to get a sense of how things are changing and how we can improve things. But presumably that can also cause people's opinions to solidify [during the polling process], making further deliberation useless. So the question arises: Under which background conditions is intermittent polling useful, and under which conditions is it not useful?

I think there can be a lot of synergies between deliberative democracy research and multi-agent systems research. Multi-agent research could suggest empirical tests of deliberative practices, but empirical-diluter-of-democracy research could suggest multi-agent phenomena to model. If you’d like a primer in deliberative democracy, there was a recent article in Science called “The crisis of democracy and the science of deliberation.”

Also, here's the list of a few experts: Josh Cohen, John Dryzek, James Fishkin, Helene Landemore, and several others. Their work is a good start if you're interested in learning about deliberative democracy.

Overall, I think there are five major takeaways [from this talk]:

1. There are several social-choice results that pretty much every member of the effective altruism community should be aware of.
2. Heuristically speaking, approval voting is probably the best norm for aggregating information in a democratic fashion.
3. There are many meaningful interpretations of the majority rule, not just majority preference or consent in majority.
4. Heuristically speaking, improving democratic group decision-making should roughly entail honesty, knowledge, independence, and universal suffrage. You want to generally promote those properties or those characteristics in the people who participate in group judgments.
5. Group decision-making becomes very complex, very quickly, and it's useful and urgent to have multi-agent research in this field to better understand these issues.

Finally, I love each and every one of you, and I look forward to learning from all of you. Have a good day.